Master the Calculation of Capacitor Charges with Expert Tips.
A capacitor is a device that is used to store electrical charge and electrical energy. A basic capacitor consists of two metal plates separated by some insulator called a dielectric. The ability of a capacitor to hold a charge is called capacitance.
When battery terminals are connected across a capacitor, battery potential will move the charge and it will begin to accumulate on the plates of the capacitor. The terminal of the capacitor that is connected to the cathode of the battery will get positively charged (+Q) and the terminal that is connected to the anode of the battery will get negatively charged (-Q). capacitor remains neutral overall but charges are separated on opposite plates that are a set distance from each other with a distance (d). A basic capacitor is shown in Fig. 1
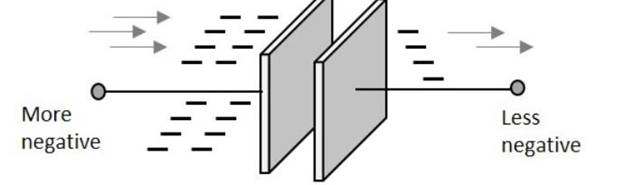
Fig. 1
The charge stored on the plates of the capacitor is directly proportional to the applied voltage so [1]
V α Q
Where
V = Voltage
Q = Charge
Capacitors with different physical parameters can hold different amounts of charge when the same amount of voltages are applied across the capacitors. This ability of the capacitor is called capacitance. The capacitance of a capacitor can be defined as the ratio of the amount of maximum charge (Q) that a capacitor can store to the applied voltage (V).
V = C Q
Q = C V
So the amount of charge on a capacitor can be determined using the above-mentioned formula.
Capacitors charges in a predictable way, and it takes time for the capacitor to charge. Considering the charging as a function of time we can also determine the amount of charge on a capacitor after a certain period of time when it is connected across the battery as shown in Fig. 2
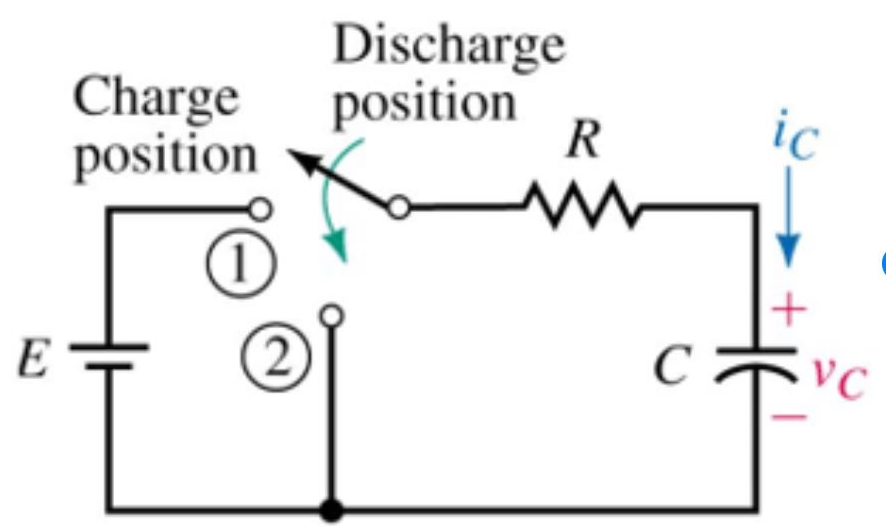
Fig. 2 Capacitor connected in RC circuit
Assume capacitor (C) is fully discharged and the switch is open, there will no charge on the capacitor. This situation represents a scenario where at t=0, I=0, and charge stored on capacitor C will also be zero.
Now as soon as the switch is closed, current will begin to flow through the circuit, the maximum amount of current that will flow through the circuit is restricted by the resistor (R) that is connected in series with the capacitor. Current that will flow through the circuit can be found using Kirchhoff’s voltage law [2]
where
V = Voltage
I(t) = Current through the circuit at any instant of time
Vc = Voltage across capacitor
Q = Charge
C = Capacitance connected in the circuit
R = Resistance connected in the circuit
V = I(t) R + Q/C
Q = CV [ 1-e-t/RC ]
The amount of charge at any instant can be found using the above-mentioned equation. A graph for the charging of the capacitor is shown in Fig. 3
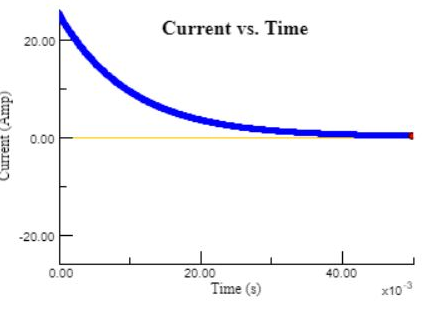
Fig. 3 Charging of capacitor with respect to time
From the graph, it can be told that initially charging current will be maximum and the capacitor will begin to change rapidly, and after a one-time constant that is T=RC capacitor will charge approximately 63% of its total value. The capacitor will keep on charging, the charging current will decrease and the rate at which the capacitor was charging will also reduce.
After a five-time constant, the capacitor will be fully charged and the charging current will be zero. Considering the charge on the capacitor as a function of time when it is connected in the circuit, the amount of charge at any time instant can be found.
Reference
[1] Basic Electrical Engineering by V.K. Mehta, Rohit Mehta, page 296
[2] Capacitors by R.P. Deshpande, page 29
